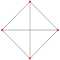
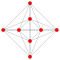
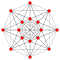
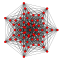
In geometry, demihypercubes (also called n-demicubes, n-hemicubes, and half measure polytopes) are a class of n-polytopes constructed from alternation of an n-hypercube, labeled as hγ_n for being half of the hypercube family, γ_n. Half of the vertices are deleted and new facets are formed. The 2n facets become 2n (n−1)-demicubes, and 2ⁿ (n−1)-simplex facets are formed in place of the deleted vertices.^[1]

They have been named with a demi- prefix to each hypercube name: demicube, demitesseract, etc. The demicube is identical to the regular tetrahedron, and the demitesseract is identical to the regular 16-cell. The demipenteract is considered semiregular for having only regular facets. Higher forms do not have all regular facets but are all uniform polytopes.

The vertices and edges of a demihypercube form two copies of the halved cube graph.

An n-demicube has inversion symmetry if n is even.

Thorold Gosset described the demipenteract in his 1900 publication listing all of the regular and semiregular figures in n-dimensions above three. He called it a 5-ic semi-regular. It also exists within the semiregular k₂₁ polytope family.

The demihypercubes can be represented by extended Schläfli symbols of the form h{4,3,...,3} as half the vertices of {4,3,...,3}. The vertex figures of demihypercubes are rectified n-simplexes.

They are represented by Coxeter-Dynkin diagrams of three constructive forms:

1. ... (As an alternated orthotope) s{2^1,1,...,1}
2. ... (As an alternated hypercube) h{4,3ⁿ⁻¹}
3. .... (As a demihypercube) {3^1,n−3,1}

H.S.M. Coxeter also labeled the third bifurcating diagrams as 1_k1 representing the lengths of the three branches and led by the ringed branch.

An n-demicube, n greater than 2, has n(n−1)/2 edges meeting at each vertex. The graphs below show less edges at each vertex due to overlapping edges in the symmetry projection.

More information n, 1k1 ...

n	1k1	Petrie polygon	Schläfli symbol	Coxeter diagrams A1n Bn Dn	Elements										Facets: Demihypercubes & Simplexes	Vertex figure
					Vertices	Edges	Faces	Cells	4-faces	5-faces	6-faces	7-faces	8-faces	9-faces
2	1−1,1	demisquare (digon)	s{2} h{4} {31,−1,1}		2	2									2 edges	--
3	101	demicube (tetrahedron)	s{21,1} h{4,3} {31,0,1}		4	6	4								(6 digons) 4 triangles	Triangle (Rectified triangle)
4	111	demitesseract (16-cell)	s{21,1,1} h{4,3,3} {31,1,1}		8	24	32	16							8 demicubes (tetrahedra) 8 tetrahedra	Octahedron (Rectified tetrahedron)
5	121	demipenteract	s{21,1,1,1} h{4,33}{31,2,1}		16	80	160	120	26						10 16-cells 16 5-cells	Rectified 5-cell
6	131	demihexeract	s{21,1,1,1,1} h{4,34}{31,3,1}		32	240	640	640	252	44					12 demipenteracts 32 5-simplices	Rectified hexateron
7	141	demihepteract	s{21,1,1,1,1,1} h{4,35}{31,4,1}		64	672	2240	2800	1624	532	78				14 demihexeracts 64 6-simplices	Rectified 6-simplex
8	151	demiocteract	s{21,1,1,1,1,1,1} h{4,36}{31,5,1}		128	1792	7168	10752	8288	4032	1136	144			16 demihepteracts 128 7-simplices	Rectified 7-simplex
9	161	demienneract	s{21,1,1,1,1,1,1,1} h{4,37}{31,6,1}		256	4608	21504	37632	36288	23520	9888	2448	274		18 demiocteracts 256 8-simplices	Rectified 8-simplex
10	171	demidekeract	s{21,1,1,1,1,1,1,1,1} h{4,38}{31,7,1}		512	11520	61440	122880	142464	115584	64800	24000	5300	532	20 demienneracts 512 9-simplices	Rectified 9-simplex
...
n	1n−3,1	n-demicube	s{21,1,...,1} h{4,3n−2}{31,n−3,1}	... ... ...	2n−1										2n (n−1)-demicubes 2n−1 (n−1)-simplices	Rectified (n−1)-simplex

Close

In general, a demicube's elements can be determined from the original n-cube: (with C_n,m = m^th-face count in n-cube = 2^n−m n!/(m!(n−m)!))

• Vertices: D_n,0 = 1/2 C_n,0 = 2ⁿ⁻¹ (Half the n-cube vertices remain)
• Edges: D_n,1 = C_n,2 = 1/2 n(n−1) 2ⁿ⁻² (All original edges lost, each square faces create a new edge)
• Faces: D_n,2 = 4 * C_n,3 = 2/3 n(n−1)(n−2) 2ⁿ⁻³ (All original faces lost, each cube creates 4 new triangular faces)
• Cells: D_n,3 = C_n,3 + 2³ C_n,4 (tetrahedra from original cells plus new ones)
• Hypercells: D_n,4 = C_n,4 + 2⁴ C_n,5 (16-cells and 5-cells respectively)
• ...
• [For m = 3,...,n−1]: D_n,m = C_n,m + 2^m C_n,m+1 (m-demicubes and m-simplexes respectively)
• ...
• Facets: D_n,n−1 = 2n + 2ⁿ⁻¹ ((n−1)-demicubes and (n−1)-simplices respectively)

The stabilizer of the demihypercube in the hyperoctahedral group (the Coxeter group ${\displaystyle BC_{n}}$ [4,3ⁿ⁻¹]) has index 2. It is the Coxeter group ${\displaystyle D_{n},}$ [3^n−3,1,1] of order ${\displaystyle 2^{n-1}n!}$, and is generated by permutations of the coordinate axes and reflections along pairs of coordinate axes.^[2]

Constructions as alternated orthotopes have the same topology, but can be stretched with different lengths in n-axes of symmetry.

The rhombic disphenoid is the three-dimensional example as alternated cuboid. It has three sets of edge lengths, and scalene triangle faces.

• Hypercube honeycomb
• Semiregular E-polytope