Geometric_series
Geometric series
Sum of an (infinite) geometric progression
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series
is geometric, because each successive term can be obtained by multiplying the previous term by 



The name geometric series indicates each term is the geometric mean of its two neighboring terms, similar to how the name arithmetic series indicates each term is the arithmetic mean of its two neighboring terms.
Coefficient a

The geometric series a + ar + ar2 + ar3 + ... is written in expanded form.[1] Every coefficient in the geometric series is the same. In contrast, the power series written as a0 + a1r + a2r2 + a3r3 + ... in expanded form has coefficients ai that can vary from term to term. In other words, the geometric series is a special case of the power series. The first term of a geometric series in expanded form is the coefficient a of that geometric series.
In addition to the expanded form of the geometric series, there is a generator form[1] of the geometric series written as
and a closed form of the geometric series written as
The derivation of the closed form from the expanded form is shown in this article's § Sum section. However even without that derivation, the result can be confirmed with long division: a divided by (1 - r) results in a + ar + ar2 + ar3 + ... , which is the expanded form of the geometric series.
It is often a convenience in notation to set the series equal to the sum s and work with the geometric series
- s = a + ar + ar2 + ar3 + ar4 + ... in its normalized form
- s / a = 1 + r + r2 + r3 + r4 + ... or in its normalized vector form
- s / a = [1 1 1 1 1 ...][1 r r2 r3 r4 ...]T or in its normalized partial series form
- sn / a = 1 + r + r2 + r3 + r4 + ... + rn, where n is the power (or degree) of the last term included in the partial sum sn.
Changing even one of the coefficients to something other than coefficient a would change the resulting sum of functions to some function other than a / (1 − r) within the range |r| < 1. As an aside, a particularly useful change to the coefficients is defined by the Taylor series, which describes how to change the coefficients so that the sum of functions converges to any user selected, sufficiently smooth function within a range.
Common ratio r
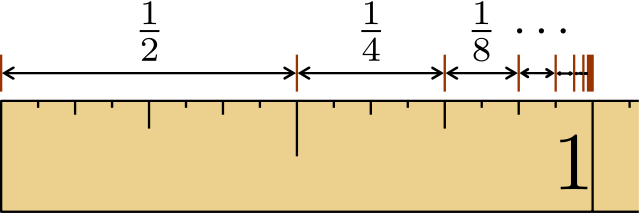


The geometric series a + ar + ar2 + ar3 + ... is an infinite series defined by just two parameters: coefficient a and common ratio r. Common ratio r is the ratio of any term with the previous term in the series. Or equivalently, common ratio r is the term multiplier used to calculate the next term in the series. The following table shows several geometric series:
| a | r | Example series |
|---|---|---|
| 4 | 10 | 4 + 40 + 400 + 4000 + 40,000 + ··· |
| 3 | 1 | 3 + 3 + 3 + 3 + 3 + ··· |
| 1 | 2/3 | 1 + 2/3 + 4/9 + 8/27 + 16/81 + ··· |
| 1/2 | 1/2 | 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ··· |
| 9 | 1/3 | 9 + 3 + 1 + 1/3 + 1/9 + ··· |
| 7 | 1/10 | 7 + 0.7 + 0.07 + 0.007 + 0.0007 + ··· |
| 1 | −1/2 | 1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + ··· |
| 3 | −1 | 3 − 3 + 3 − 3 + 3 − ··· |
The convergence of the geometric series depends on the value of the common ratio r:
- If |r| < 1, the terms of the series approach zero in the limit (becoming smaller and smaller in magnitude), and the series converges to the sum a / (1 - r).
- If |r| = 1, the series does not converge. When r = 1, all of the terms of the series are the same and the series is infinite. When r = −1, the terms take two values alternately (for example, 2, −2, 2, −2, 2,... ). The sum of the terms oscillates between two values (for example, 2, 0, 2, 0, 2,... ). This is a different type of divergence. See for example Grandi's series: 1 − 1 + 1 − 1 + ···.
- If |r| > 1, the terms of the series become larger and larger in magnitude. The sum of the terms also gets larger and larger, and the series does not converge to a sum. (The series diverges.)
The rate of convergence also depends on the value of the common ratio r. Specifically, the rate of convergence gets slower as r approaches 1 or −1. For example, the geometric series with a = 1 is 1 + r + r2 + r3 + ... and converges to 1 / (1 - r) when |r| < 1. However, the number of terms needed to converge approaches infinity as r approaches 1 because a / (1 - r) approaches infinity and each term of the series is less than or equal to one. In contrast, as r approaches −1 the sum of the first several terms of the geometric series starts to converge to 1/2 but slightly flips up or down depending on whether the most recently added term has a power of r that is even or odd. That flipping behavior near r = −1 is illustrated in the adjacent image showing the first 11 terms of the geometric series with a = 1 and |r| < 1.
The common ratio r and the coefficient a also define the geometric progression, which is a list of the terms of the geometric series but without the additions. Therefore the geometric series a + ar + ar2 + ar3 + ... has the geometric progression (also called the geometric sequence) a, ar, ar2, ar3, ... The geometric progression - as simple as it is - models a surprising number of natural phenomena,
- from some of the largest observations such as the expansion of the universe where the common ratio r is defined by Hubble's constant,
- to some of the smallest observations such as the decay of radioactive carbon-14 atoms where the common ratio r is defined by the half-life of carbon-14.
As an aside, the common ratio r can be a complex number such as |r|eiθ where |r| is the vector's magnitude (or length), θ is the vector's angle (or orientation) in the complex plane and i2 = -1. With a common ratio |r|eiθ, the expanded form of the geometric series is a + a|r|eiθ + a|r|2ei2θ + a|r|3ei3θ + ... Modeling the angle θ as linearly increasing over time at the rate of some angular frequency ω0 (in other words, making the substitution θ = ω0t), the expanded form of the geometric series becomes a + a|r|eiω0t + a|r|2ei2ω0t + a|r|3ei3ω0t + ... , where the first term is a vector of length a not rotating at all, and all the other terms are vectors of different lengths rotating at harmonics of the fundamental angular frequency ω0. The constraint |r|<1 is enough to coordinate this infinite number of vectors of different lengths all rotating at different speeds into tracing a circle, as shown in the adjacent video. Similar to how the Taylor series describes how to change the coefficients so the series converges to a user selected sufficiently smooth function within a range, the Fourier series describes how to change the coefficients (which can also be complex numbers in order to specify the initial angles of vectors) so the series converges to a user selected periodic function.
The sum of the first n terms of a geometric series, up to and including the r n-1 term, is given by the closed-form formula:

where r is the common ratio. One can derive that closed-form formula for the partial sum, sn, by subtracting out the many self-similar terms as follows:[3][4][5]

As n approaches infinity, the absolute value of r must be less than one for the series to converge. The sum then becomes

The formula also holds for complex r, with the corresponding restriction that the modulus of r is strictly less than one.
As an aside, the question of whether an infinite series converges is fundamentally a question about the distance between two values: given enough terms, does the value of the partial sum get arbitrarily close to the finite value it is approaching? In the above derivation of the closed form of the geometric series, the interpretation of the distance between two values is the distance between their locations on the number line. That is the most common interpretation of the distance between two values. However, the p-adic metric, which has become a critical notion in modern number theory, offers a definition of distance such that the geometric series 1 + 2 + 4 + 8 + ... with a = 1 and r = 2 actually does converge to a / (1 - r) = 1 / (1 - 2) = -1 even though r is outside the typical convergence range |r| < 1.
Proof of convergence
We can prove that the geometric series converges using the sum formula for a geometric progression:

The second equality is true because if 



Alternatively, a geometric interpretation of the convergence is shown in the adjacent diagram. The area of the white triangle is the series remainder = s − sn = arn+1 / (1 − r). Each additional term in the partial series reduces the area of that white triangle remainder by the area of the trapezoid representing the added term. The trapezoid areas (i.e., the values of the terms) get progressively thinner and shorter and closer to the origin. In the limit, as the number of trapezoids approaches infinity, the white triangle remainder vanishes as it is filled by trapezoids and therefore sn converges to s, provided |r|<1. In contrast, if |r|>1, the trapezoid areas representing the terms of the series instead get progressively wider and taller and farther from the origin, not converging to the origin and not converging as a series.
Rate of convergence
After knowing that a series converges, there are some applications in which it is also important to know how quickly the series converges. For the geometric series, one convenient measure of the convergence rate is how much the previous series remainder decreases due to the last term of the partial series. Given that the last term is arn and the previous series remainder is s - sn-1 = arn / (1 - r)), this measure of the convergence rate of the geometric series is arn / (arn / (1 - r)) = 1 - r, if 0 ≤ r < 1.
If r < 0, adjacent terms in the geometric series alternate between being positive and negative. A geometric interpretation of a converging alternating geometric series is shown in the adjacent diagram in which the areas of the negative terms are shown below the x axis. Pairing and summing each positive area with its negative smaller area neighbor results in non-overlapped trapezoids separated by gaps. To remove the gaps, broaden each trapezoid to cover the rightmost 1 - r2 of the original triangle area instead of just the rightmost 1 - |r|. However, to maintain the same trapezoid areas during this broadening transformation, scaling is needed: scale*(1 - r2) = (1 - |r|), or scale = (1 - |r|) / (1 - r2) = (1 + r) / (1 - r2) = (1 + r) / ((1 + r)(1 - r)) = 1 / (1 - r) where -1 < r ≤ 0. Note that because r < 0 this scale decreases the amplitude of the separated trapezoids in order to fill in the separation gaps. In contrast, for the case r > 0 the same scale 1 / (1 - r) increases the amplitude of the non-overlapped trapezoids in order to account for the loss of the overlapped areas.
With the gaps removed, pairs of terms in a converging alternating geometric series become a converging (non-alternating) geometric series with common ratio r2 to account for the pairing of terms, coefficient a = 1 / (1 - r) to account for the gap filling, and the degree (i.e., highest powered term) of the partial series called m instead of n to emphasize that terms have been paired. Similar to the r > 0 case, the r < 0 convergence rate = ar2m / (s - sm-1) = 1 - r2, which is the same as the convergence rate of a non-alternating geometric series if its terms were similarly paired. Therefore, the convergence rate does not depend upon n or m and, perhaps more surprising, does not depend upon the sign of the common ratio. One perspective that helps explain the variable rate of convergence that is symmetric about r = 0 is that each added term of the partial series makes a finite contribution to the infinite sum at r = 1 and each added term of the partial series makes a finite contribution to the infinite slope at r = -1.
Derivation
Finite series
To derive this formula, first write a general geometric series as:

We can find a simpler formula for this sum by multiplying both sides of the above equation by 1 − r, and we'll see that

since all the other terms cancel. If r ≠ 1, we can rearrange the above to get the convenient formula for a geometric series that computes the sum of n terms:

- Related formulas
If one were to begin the sum not from k=1 or 0 but from a different value, say 

Differentiating this formula with respect to 

For example:

For a geometric series containing only even powers of 


Equivalently, take 
For a series with only odd powers of 

An exact formula for the generalized sum 

![{\displaystyle G_{s}(n,r)=\sum _{j=0}^{s}\left\lbrace {s \atop j}\right\rbrace x^{j}{\frac {d^{j}}{dx^{j}}}\left[{\frac {1-x^{n+1}}{1-x}}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cf0345d5017a50622293433e999cc9a6f161b81c)
Infinite series
An infinite geometric series is an infinite series whose successive terms have a common ratio. Such a series converges if and only if the absolute value of the common ratio is less than one (|r| < 1). Its value can then be computed from the finite sum formula

 (red line) to its sum
(red line) to its sum  (blue line) for
(blue line) for  .
.Since:

Then:

For a series containing only even powers of 

and for odd powers only,

In cases where the sum does not start at k = 0,

The formulae given above are valid only for |r| < 1. The latter formula is valid in every Banach algebra, as long as the norm of r is less than one, and also in the field of p-adic numbers if |r|p < 1. As in the case for a finite sum, we can differentiate to calculate formulae for related sums. For example,

This formula only works for |r| < 1 as well. From this, it follows that, for |r| < 1,

Also, the infinite series 1/2 + 1/4 + 1/8 + 1/16 + ⋯ is an elementary example of a series that converges absolutely.
It is a geometric series whose first term is 1/2 and whose common ratio is 1/2, so its sum is

The inverse of the above series is 1/2 − 1/4 + 1/8 − 1/16 + ⋯ is a simple example of an alternating series that converges absolutely.
It is a geometric series whose first term is 1/2 and whose common ratio is −1/2, so its sum is

Complex series
The summation formula for geometric series remains valid even when the common ratio is a complex number. In this case the condition that the absolute value of r be less than 1 becomes that the modulus of r be less than 1. It is possible to calculate the sums of some non-obvious geometric series. For example, consider the proposition

The proof of this comes from the fact that

which is a consequence of Euler's formula. Substituting this into the original series gives
![{\displaystyle \sum _{k=0}^{\infty }{\frac {\sin(kx)}{r^{k}}}={\frac {1}{2i}}\left[\sum _{k=0}^{\infty }\left({\frac {e^{ix}}{r}}\right)^{k}-\sum _{k=0}^{\infty }\left({\frac {e^{-ix}}{r}}\right)^{k}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/25cf9f93893b1fd2d73c263c64a6850720217bca)
This is the difference of two geometric series, and so it is a straightforward application of the formula for infinite geometric series that completes the proof.
Zeno of Elea (c.495 – c.430 BC)
2,500 years ago, Greek mathematicians had a problem when walking from one place to another: they thought[7] that an infinitely long list of numbers greater than zero summed to infinity. Therefore, it was a paradox when Zeno of Elea pointed out that in order to walk from one place to another, you first have to walk half the distance, and then you have to walk half the remaining distance, and then you have to walk half of that remaining distance, and you continue halving the remaining distances an infinite number of times because no matter how small the remaining distance is you still have to walk the first half of it. Thus, Zeno of Elea transformed a short distance into an infinitely long list of halved remaining distances, all of which are greater than zero. And that was the problem: how can a distance be short when measured directly and also infinite when summed over its infinite list of halved remainders? The paradox revealed something was wrong with the assumption that an infinitely long list of numbers greater than zero summed to infinity.
Euclid of Alexandria (c.300 BC)
Euclid's Elements of Geometry[8] Book IX, Proposition 35, proof (of the proposition in adjacent diagram's caption):
Let AA', BC, DD', EF be any multitude whatsoever of continuously proportional numbers, beginning from the least AA'. And let BG and FH, each equal to AA', have been subtracted from BC and EF. I say that as GC is to AA', so EH is to AA', BC, DD'.
For let FK be made equal to BC, and FL to DD'. And since FK is equal to BC, of which FH is equal to BG, the remainder HK is thus equal to the remainder GC. And since as EF is to DD', so DD' to BC, and BC to AA' [Prop. 7.13], and DD' equal to FL, and BC to FK, and AA' to FH, thus as EF is to FL, so LF to FK, and FK to FH. By separation, as EL to LF, so LK to FK, and KH to FH [Props. 7.11, 7.13]. And thus as one of the leading is to one of the following, so (the sum of) all of the leading to (the sum of) all of the following [Prop. 7.12]. Thus, as KH is to FH, so EL, LK, KH to LF, FK, HF. And KH equal to CG, and FH to AA', and LF, FK, HF to DD', BC, AA'. Thus, as CG is to AA', so EH to DD', BC, AA'. Thus, as the excess of the second is to the first, so is the excess of the last is to all those before it. The very thing it was required to show.
The terseness of Euclid's propositions and proofs may have been a necessity. As is, the Elements of Geometry is over 500 pages of propositions and proofs. Making copies of this popular textbook was labor intensive given that the printing press was not invented until 1440. And the book's popularity lasted a long time: as stated in the cited introduction to an English translation, Elements of Geometry "has the distinction of being the world's oldest continuously used mathematical textbook." So being very terse was being very practical. The proof of Proposition 35 in Book IX could have been even more compact if Euclid could have somehow avoided explicitly equating lengths of specific line segments from different terms in the series. For example, the contemporary notation for geometric series (i.e., a + ar + ar2 + ar3 + ... + arn) does not label specific portions of terms that are equal to each other.
Also in the cited introduction the editor comments,
Most of the theorems appearing in the Elements were not discovered by Euclid himself, but were the work of earlier Greek mathematicians such as Pythagoras (and his school), Hippocrates of Chios, Theaetetus of Athens, and Eudoxus of Cnidos. However, Euclid is generally credited with arranging these theorems in a logical manner, so as to demonstrate (admittedly, not always with the rigour demanded by modern mathematics) that they necessarily follow from five simple axioms. Euclid is also credited with devising a number of particularly ingenious proofs of previously discovered theorems (e.g., Theorem 48 in Book 1).
To help translate the proposition and proof into a form that uses current notation, a couple modifications are in the diagram. First, the four horizontal line lengths representing the values of the first four terms of a geometric series are now labeled a, ar, ar2, ar3 in the diagram's left margin. Second, new labels A' and D' are now on the first and third lines so that all the diagram's line segment names consistently specify the segment's starting point and ending point.
Here is a phrase by phrase interpretation of the proposition:
| Proposition | in contemporary notation |
|---|---|
| "If there is any multitude whatsoever of continually proportional numbers" | Taking the first n+1 terms of a geometric series Sn = a + ar + ar2 + ar3 + ... + arn |
| "and equal to the first is subtracted from the second and the last" | and subtracting a from ar and arn |
| "then as the excess of the second to the first, so the excess of the last will be to all those before it." | then (ar-a) / a = (arn-a) / (a + ar + ar2 + ar3 + ... + arn-1) = (arn-a) / Sn-1, which can be rearranged to the more familiar form Sn-1 = a(rn-1) / (r-1). |
Similarly, here is a sentence by sentence interpretation of the proof:
| Proof | in contemporary notation |
|---|---|
| "Let AA', BC, DD', EF be any multitude whatsoever of continuously proportional numbers, beginning from the least AA'." | Consider the first n+1 terms of a geometric series Sn = a + ar + ar2 + ar3 + ... + arn for the case r>1 and n=3. |
| "And let BG and FH, each equal to AA', have been subtracted from BC and EF." | Subtract a from ar and ar3. |
| "I say that as GC is to AA', so EH is to AA', BC, DD'." | I say that (ar-a) / a = (ar3-a) / (a + ar + ar2). |
| "For let FK be made equal to BC, and FL to DD'." | |
| "And since FK is equal to BC, of which FH is equal to BG, the remainder HK is thus equal to the remainder GC." | |
| "And since as EF is to DD', so DD' to BC, and BC to AA' [Prop. 7.13], and DD' equal to FL, and BC to FK, and AA' to FH, thus as EF is to FL, so LF to FK, and FK to FH." | |
| "By separation, as EL to LF, so LK to FK, and KH to FH [Props. 7.11, 7.13]." | By separation, (ar3-ar2) / ar2 = (ar2-ar) / ar = (ar-a) / a = r-1. |
| "And thus as one of the leading is to one of the following, so (the sum of) all of the leading to (the sum of) all of the following [Prop. 7.12]." | The sum of those numerators and the sum of those denominators form the same proportion: ((ar3-ar2) + (ar2-ar) + (ar-a)) / (ar2 + ar + a) = r-1. |
| "And thus as one of the leading is to one of the following, so (the sum of) all of the leading to (the sum of) all of the following [Prop. 7.12]." | And this sum of equal proportions can be extended beyond (ar3-ar2) / ar2 to include all the proportions up to (arn-arn-1) / arn-1. |
| "Thus, as KH is to FH, so EL, LK, KH to LF, FK, HF." | |
| "And KH equal to CG, and FH to AA', and LF, FK, HF to DD', BC, AA'." | |
| "Thus, as CG is to AA', so EH to DD', BC, AA'." | |
| "Thus, as the excess of the second is to the first, so is the excess of the last is to all those before it." | Thus, (ar-a) / a = (ar3-a) / S2. Or more generally, (ar-a) / a = (arn-a) / Sn-1, which can be rearranged in the more common form Sn-1 = a(rn-1) / (r-1). |
| "The very thing it was required to show." | Q.E.D. |
Archimedes of Syracuse (c.287 – c.212 BC)
Archimedes used the sum of a geometric series to compute the area enclosed by a parabola and a straight line. His method was to dissect the area into an infinite number of triangles.
Archimedes' Theorem states that the total area under the parabola is 4/3 of the area of the blue triangle.
Archimedes determined that each green triangle has 1/8 the area of the blue triangle, each yellow triangle has 1/8 the area of a green triangle, and so forth.
Assuming that the blue triangle has area 1, the total area is an infinite sum:
The first term represents the area of the blue triangle, the second term the areas of the two green triangles, the third term the areas of the four yellow triangles, and so on. Simplifying the fractions gives
This is a geometric series with common ratio 1/4 and the fractional part is equal to
The sum is
This computation uses the method of exhaustion, an early version of integration. Using calculus, the same area could be found by a definite integral.
Nicole Oresme (c.1323 – 1382)
Among his insights into infinite series, in addition to his elegantly simple proof of the divergence of the harmonic series, Nicole Oresme[9] proved that the series 1/2 + 2/4 + 3/8 + 4/16 + 5/32 + 6/64 + 7/128 + ... converges to 2. His diagram for his geometric proof, similar to the adjacent diagram, shows a two dimensional geometric series. The first dimension is horizontal, in the bottom row showing the geometric series S = 1/2 + 1/4 + 1/8 + 1/16 + ... , which is the geometric series with coefficient a = 1/2 and common ratio r = 1/2 that converges to S = a / (1-r) = (1/2) / (1-1/2) = 1. The second dimension is vertical, where the bottom row is a new coefficient aT equal to S and each subsequent row above it is scaled by the same common ratio r = 1/2, making another geometric series T = 1 + 1/2 + 1/4 + 1/8 + ..., which is the geometric series with coefficient aT = S = 1 and common ratio r = 1/2 that converges to T = aT / (1-r) = S / (1-r) = a / (1-r) / (1-r) = (1/2) / (1-1/2) / (1-1/2) = 2.
Although difficult to visualize beyond three dimensions, Oresme's insight generalizes to any dimension d. Using the sum of the d−1 dimension of the geometric series as the coefficient a in the d dimension of the geometric series results in a d-dimensional geometric series converging to Sd / a = 1 / (1-r)d within the range |r|<1. Pascal's triangle and long division reveals the coefficients of these multi-dimensional geometric series, where the closed form is valid only within the range |r|<1.
 ...
...  |
 (closed form) (closed form) |  (expanded form) (expanded form) |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
As an aside, instead of using long division, it is also possible to calculate the coefficients of the d-dimensional geometric series by integrating the coefficients of dimension d−1. This mapping from division by 1-r in the power series sum domain to integration in the power series coefficient domain is a discrete form of the mapping performed by the Laplace transform. MIT Professor Arthur Mattuck shows how to derive the Laplace transform from the power series in this lecture video,[10] where the power series is a mapping between discrete coefficients and a sum and the Laplace transform is a mapping between continuous weights and an integral.
Economics
In economics, geometric series are used to represent the present value of an annuity (a sum of money to be paid in regular intervals).
For example, suppose that a payment of $100 will be made to the owner of the annuity once per year (at the end of the year) in perpetuity. Receiving $100 a year from now is worth less than an immediate $100, because one cannot invest the money until one receives it. In particular, the present value of $100 one year in the future is $100 / (1 + 

Similarly, a payment of $100 two years in the future has a present value of $100 / (1 + 
which is the infinite series:
This is a geometric series with common ratio 1 / (1 + 
For example, if the yearly interest rate is 10% (
This sort of calculation is used to compute the APR of a loan (such as a mortgage loan). It can also be used to estimate the present value of expected stock dividends, or the terminal value of a financial asset assuming a stable growth rate.
Fractal geometry
The area inside the Koch snowflake can be described as the union of infinitely many equilateral triangles (see figure). Each side of the green triangle is exactly 1/3 the size of a side of the large blue triangle, and therefore has exactly 1/9 the area. Similarly, each yellow triangle has 1/9 the area of a green triangle, and so forth. Taking the blue triangle as a unit of area, the total area of the snowflake is
The first term of this series represents the area of the blue triangle, the second term the total area of the three green triangles, the third term the total area of the twelve yellow triangles, and so forth. Excluding the initial 1, this series is geometric with constant ratio r = 4/9. The first term of the geometric series is a = 3(1/9) = 1/3, so the sum is
Thus the Koch snowflake has 8/5 of the area of the base triangle.
Integration
The derivative of ![{\displaystyle f(x)=\arctan(u(x)){\text{ is }}f'(x)=u'(x)/(1+[u(x)]^{2})}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0eb96e30b5fb00c46b86214ae1895e618256d494)
Therefore, letting 
which is called Gregory's series and is commonly attributed to Madhava of Sangamagrama (c. 1340 – c. 1425).
- Grandi's series – The infinite sum of alternating 1 and -1 terms: 1 − 1 + 1 − 1 + ⋯
- 1 + 2 + 4 + 8 + ⋯ – Infinite series
- 1 − 2 + 4 − 8 + ⋯ – infinite seriesPages displaying wikidata descriptions as a fallback
- 1/2 + 1/4 + 1/8 + 1/16 + ⋯ – Mathematical infinite series
- 1/2 − 1/4 + 1/8 − 1/16 + ⋯ – mathematical infinite seriesPages displaying wikidata descriptions as a fallback
- 1/4 + 1/16 + 1/64 + 1/256 + ⋯ – Infinite sum equal to 1/3 at its limit
- A geometric series is a unit series (the series sum converges to one) if and only if |r| < 1 and a + r = 1 (equivalent to the more familiar form S = a / (1 - r) = 1 when |r| < 1). Therefore, an alternating series is also a unit series when -1 < r < 0 and a + r = 1 (for example, coefficient a = 1.7 and common ratio r = -0.7).
- The terms of a geometric series are also the terms of a generalized Fibonacci sequence (Fn = Fn-1 + Fn-2 but without requiring F0 = 0 and F1 = 1) when a geometric series common ratio r satisfies the constraint 1 + r = r2, which according to the quadratic formula is when the common ratio r equals the golden ratio (i.e., common ratio r = (1 ± √5)/2).
- The only geometric series that is a unit series and also has terms of a generalized Fibonacci sequence has the golden ratio as its coefficient a and the conjugate golden ratio as its common ratio r (i.e., a = (1 + √5)/2 and r = (1 - √5)/2). It is a unit series because a + r = 1 and |r| < 1, it is a generalized Fibonacci sequence because 1 + r = r2, and it is an alternating series because r < 0.
Geometric series
The geometric series has two degrees of freedom: one for its coefficient a and another for its common ratio r. In the map of polynomials, the big red circle represents the set of all geometric series.
Converging geometric series
Only a subset of all geometric series converge. Specifically, a geometric series converges if and only if its common ratio |r| < 1. In the map of polynomials, the red triangle represents the set of converging geometric series and being drawn inside the big red circle representing the set of all geometric series indicates the converging geometric series is a subset of the geometric series.
Repeated decimals
Only a subset of all converging geometric series converge to decimal fractions that have repeated patterns that continue forever (e.g., 0.7777... or 0.9999... or 0.123412341234...). In the map of polynomials, the little yellow triangle represents the set of geometric series that converge to infinitely repeated decimal patterns. It is drawn inside the red triangle to indicate it is a subset of the converging geometric series, which in turn is drawn inside the big red circle indicating both the converging geometric series and the geometric series that converge to infinitely repeated patterns are subsets of the geometric series.
Although fractions with infinitely repeated decimal patterns can only be approximated when encoded as floating point numbers, they can always be defined exactly as the ratio of two integers and those two integers can be calculated using the geometric series. For example, the repeated decimal fraction 0.7777... can be written as the geometric series
where coefficient a = 7/10 and common ratio r = 1/10. The geometric series closed form reveals the two integers that specify the repeated pattern:
This approach extends beyond base-ten numbers. In fact, any fraction that has an infinitely repeated pattern in base-ten numbers also has an infinitely repeated pattern in numbers written in any other base. For example, looking at the floating point encoding for the number 0.7777...
julia> bitstring(Float32(0.77777777777777777777))
"00111111010001110001110001110010"
reveals the binary fraction 0.110001110001110001... where the binary pattern 0b110001 repeats indefinitely and can be written in mostly (except for the powers) binary numbers as
where coefficient a = 0b110001 / 0b1000000 = 49 / 64 and common ratio r = 1 / 0b1000000 = 1 / 64. Using the geometric series closed form as before
You may have noticed that the floating point encoding does not capture the 0b110001 repeat pattern in the last couple (least significant) bits. This is because floating point encoding rounds the remainder instead of truncating it. Therefore, if the most significant bit of the remainder is 1, the least significant bit of the encoded fraction gets incremented and that will cause a carry if the least significant bit of the fraction is already 1, which can cause another carry if that bit of the fraction is already a 1, which can cause another carry, etc. This floating point rounding and the subsequent carry propagation explains why the floating point encoding for 0.99999... is exactly the same as the floating point encoding for 1.
julia> bitstring(Float32(0.99999999999999999999))
"00111111100000000000000000000000"
julia> bitstring(Float32(1.0))
"00111111100000000000000000000000"
As an example that has four digits in the repeated pattern, 0.123412341234... can be written as the geometric series
where coefficient a = 1234/10000 and common ratio r = 1/10000. The geometric series closed form reveals the two integers that specify the repeated pattern:
Power series
Like the geometric series, the power series has one degree of freedom for its common ratio r (along the x-axis) but has n+1 degrees of freedom for its coefficients (along the y-axis), where n represents the power of the last term in the partial series. In the map of polynomials, the big blue circle represents the set of all power series.
Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century.
The partial sum formed by the first n + 1 terms of a Taylor series is a polynomial of degree n that is called the nth Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as n increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of the infinite sequence of the Taylor polynomials. A function may differ from the sum of its Taylor series, even if its Taylor series is convergent. A function is analytic at a point x if it is equal to the sum of its Taylor series in some open interval (or open disk in the complex plane) containing x. This implies that the function is analytic at every point of the interval (or disk).Binary encoded numbers
Zeno of Elea's geometric series with coefficient a=1/2 and common ratio r=1/2 is the foundation of binary encoded approximations of fractions in digital computers. Concretely, the geometric series written in its normalized vector form is s/a = [1 1 1 1 1 …][1 r r2 r3 r4 …]T. Keeping the column vector of basis functions [1 r r2 r3 r4 …]T the same but generalizing the row vector [1 1 1 1 1 …] so that each entry can be either a 0 or a 1 allows for an approximate encoding of any fraction. For example, the value v = 0.34375 is encoded as v/a = [0 1 0 1 1 0 …][1 r r2 r3 r4 …]T where coefficient a = 1/2 and common ratio r = 1/2. Typically, the row vector is written in the more compact binary form v = 0.010110 which is 0.34375 in decimal.
Similarly, the geometric series with coefficient a=1 and common ratio r=2 is the foundation for binary encoded integers in digital computers. Again, the geometric series written in its normalized vector form is s/a = [1 1 1 1 1 …][1 r r2 r3 r4 …]T. Keeping the column vector of basis functions [1 r r2 r3 r4 …]T the same but generalizing the row vector [1 1 1 1 1 …] so that each entry can be either a 0 or a 1 allows for an encoding of any integer. For example, the value v = 151 is encoded as v/a = [1 1 1 0 1 0 0 1 0 …][1 r r2 r3 r4 r5 r6 r7 r8 …]T where coefficient a = 1 and common ratio r = 2. Typically, the row vector is written in reverse order (so that the most significant bit is first) in the more compact binary form v = …010010111 = 10010111 which is 151 in decimal.
As shown in the adjacent figure, the standard binary encoding of a 32-bit floating point number is a combination of a binary encoded integer and a binary encoded fraction, beginning at the most significant bit with
- the sign bit, followed by
- an 8-bit integer exponent field with an assumed offset of 127 (so a value of 127 represents an exponent value of 0) and with a base of 2 meaning that the exponent value specifies a bit shift of the fraction field, followed by
- a 23-bit fraction field with an assumed but not encoded 1 serving as the fraction's most significant nonzero bit which would be in bit position 23 if it were encoded.
Building upon the previous example of 0.34375 having binary encoding of 0.010110, a floating point encoding (according to the IEEE 754 standard) of 0.34375 is
- the sign bit which is 0 because the number is not negative,
- an 8-bit integer exponent field which must specify a shift that counters the 2 bit left shift to get the original binary encoding from 0.010110 to 1.0110, and that counter shift to recover the original binary encoding is a right shift of 2 bits which is specified by an exponent value of 125 (because 125 − 127 = -2 which is a right shift of 2 bits) which in binary is 0111 1101,
- a 23-bit fraction field: .0110 0000 0000 0000 0000 000.
Although encoding floating point numbers by hand like this is possible, letting a computer do it is easier and less error prone. The following Julia code confirms the hand calculated floating point encoding of the number 0.34375:
julia> bitstring(Float32(0.34375))
"00111110101100000000000000000000"
Laurent series
 and a path of integration γ. The path of integration must lie in an annulus, indicated here by the red color, inside which
and a path of integration γ. The path of integration must lie in an annulus, indicated here by the red color, inside which  is holomorphic (analytic).
is holomorphic (analytic). is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.[12]
is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.[12]
Complex Fourier series
As an example of the ability of the complex Fourier series to trace any 2D closed figure, in the adjacent animation a complex Fourier series traces the letter 'e' (for exponential). Given the intricate coordination of motions shown in the animation, a definition of the complex Fourier series can be surprisingly compact in just two equations:
where parameterized function s(t) traces some 2D closed figure in the complex plane as the parameter t progresses through the period from 0 to 1.
To help make sense of these compact equations defining the complex Fourier series, note that the complex Fourier series summation looks similar to the complex geometric series except that the complex Fourier series is basically two complex geometric series (one set of terms rotating in the positive direction and another set of terms rotating in the negative direction), and the coefficients of the complex Fourier series are complex constants that can vary from term to term. By allowing terms to rotate in either direction, the series becomes capable of tracing any 2D closed figure. In contrast, the complex geometric series has all the terms rotating in the same direction and it can trace only circles. Allowing the coefficients of the complex geometric series to vary from term to term would expand upon the shapes it can trace but all the possible shapes would still be limited to being puffy and cloud-like, not able to trace the shape of a simple line segment, for example going back and forth between 1 + i0 and -1 + i0. However, Euler's formula shows that the addition of just two terms rotating in opposite directions can trace that line segment between 1 + i0 and -1 + i0:
Concerning the complex Fourier series second equation defining how to calculate the coefficients, the coefficient of the non-rotating term c0 can be calculated by integrating the complex Fourier series first equation over the range of one period from 0 to 1. Over that range, all the rotating terms integrate to zero, leaving just c0. Similarly, any of the terms in the complex Fourier series first equation can be made to be a non-rotating term by multiplying both sides of the equation by 
Matrix polynomial
In mathematics, a matrix polynomial is a polynomial with square matrices as variables. Given an ordinary, scalar-valued polynomial
this polynomial evaluated at a matrix 
where 
Note that 

A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. A matrix polynomial identity is a matrix polynomial equation which holds for all matrices A in a specified matrix ring Mn(R).
Matrix polynomials are often demonstrated in undergraduate linear algebra classes due to their relevance in showcasing properties of linear transformations represented as matrices, most notably the Cayley-Hamilton theorem.Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the exponential map between a matrix Lie algebra and the corresponding Lie group.
Let X be an n×n real or complex matrix. The exponential of X, denoted by eX or exp(X), is the n×n matrix given by the power series

where 


Equivalently,

where I is the n×n identity matrix.
When X is an n×n diagonal matrix then exp(X) will be an n×n diagonal matrix with each diagonal element equal to the ordinary exponential applied to the corresponding diagonal element of X.- 0.999... – Alternative decimal expansion of 1
- Asymptote – Limit of the tangent line at a point that tends to infinity
- Divergent geometric series
- Generalized hypergeometric function – Family of power series in mathematics
- Geometric progression – Mathematical sequence of numbers
- Neumann series – Mathematical series
- Ratio test – Criterion for the convergence of a series
- Root test – Criterion for the convergence of an infinite series
- Series (mathematics) – Infinite sum
- Arithmetic series – Sequence of numbersPages displaying short descriptions of redirect targets
- Riddle, Douglas F. Calculus and Analytic Geometry, Second Edition Belmont, California, Wadsworth Publishing, p. 566, 1970.
- Hairer E.; Wanner G. (1996). Analysis by Its History. Springer. p. 188. Section III.2, Figure 2.1
- Abramowitz & Stegun (1972, p. 10)
- Moise (1967, p. 48)
- Protter & Morrey (1970, pp. 639–640)
- "Set Partitions: Stirling Numbers". Digital Library of Mathematical Functions. Retrieved 24 May 2018.
- Riddle, Douglas E (1974). Calculus and Analytic Geometry (2nd ed.). Wadsworth Publishing. p. 556. ISBN 053400301-X.
- Euclid; J.L. Heiberg (2007). Euclid's Elements of Geometry (PDF). Translated by Richard Fitzpatrick. Richard Fitzpatrick. ISBN 978-0615179841. Archived (PDF) from the original on 2013-08-11.
- Babb, J (2003). "Mathematical Concepts and Proofs from Nicole Oresme: Using the History of Calculus to Teach Mathematics" (PDF). Winnipeg: The Seventh International History, Philosophy and Science Teaching conference. pp. 11–12, 21. Archived (PDF) from the original on 2021-05-27.
- Mattuck, Arthur. "Lecture 19, MIT 18.03 Differential Equations, Spring 2006". MIT OpenCourseWare. Archived from the original on 2021-11-11.
- Riddle, Douglas (1974). Calculus and Analytic Geometry (second ed.). California: Wadsworth Publishing. p. 310. ISBN 0-534--00301-X.
- Rodriguez, Rubi; Kra, Irwin; Gilman, Jane P. (2012), Complex Analysis: In the Spirit of Lipman Bers, Graduate Texts in Mathematics, vol. 245, Springer, p. 12, ISBN 9781441973238.
- Sepesi, G (13 February 2022). "Zeno's Enduring Example". Towards Data Science. pp. Appendix B.
- Horn & Johnson 1990, p. 36.
- Abramowitz, M.; Stegun, I. A., eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (9th printing ed.). New York: Dover. p. 10.
- Andrews, George E. (1998). "The geometric series in calculus". The American Mathematical Monthly. 105 (1). Mathematical Association of America: 36–40. doi:10.2307/2589524. JSTOR 2589524.
- Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 278–279, 1985.
- Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 8, 1987.
- Courant, R. and Robbins, H. "The Geometric Progression." §1.2.3 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 13–14, 1996.
- Hall, Brian C. (2015), Lie groups, Lie algebras, and representations: An elementary introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3-319-13466-6
- Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6..
- James Stewart (2002). Calculus, 5th ed., Brooks Cole. ISBN 978-0-534-39339-7
- Larson, Hostetler, and Edwards (2005). Calculus with Analytic Geometry, 8th ed., Houghton Mifflin Company. ISBN 978-0-618-50298-1
- Moise, Edwin E. (1967), Calculus: Complete, Reading: Addison-Wesley
- Pappas, T. "Perimeter, Area & the Infinite Series." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 134–135, 1989.
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
- Roger B. Nelsen (1997). Proofs without Words: Exercises in Visual Thinking, The Mathematical Association of America. ISBN 978-0-88385-700-7
History and philosophy
- C. H. Edwards Jr. (1994). The Historical Development of the Calculus, 3rd ed., Springer. ISBN 978-0-387-94313-8.
- Swain, Gordon and Thomas Dence (April 1998). "Archimedes' Quadrature of the Parabola Revisited". Mathematics Magazine. 71 (2): 123–30. doi:10.2307/2691014. JSTOR 2691014.
- Eli Maor (1991). To Infinity and Beyond: A Cultural History of the Infinite, Princeton University Press. ISBN 978-0-691-02511-7
- Morr Lazerowitz (2000). The Structure of Metaphysics (International Library of Philosophy), Routledge. ISBN 978-0-415-22526-7
Economics
- Carl P. Simon and Lawrence Blume (1994). Mathematics for Economists, W. W. Norton & Company. ISBN 978-0-393-95733-4
- Mike Rosser (2003). Basic Mathematics for Economists, 2nd ed., Routledge. ISBN 978-0-415-26784-7
Biology
- Edward Batschelet (1992). Introduction to Mathematics for Life Scientists, 3rd ed., Springer. ISBN 978-0-387-09648-3
- Richard F. Burton (1998). Biology by Numbers: An Encouragement to Quantitative Thinking, Cambridge University Press. ISBN 978-0-521-57698-7
Computer science
- John Rast Hubbard (2000). Schaum's Outline of Theory and Problems of Data Structures With Java, McGraw-Hill. ISBN 978-0-07-137870-3
- "Geometric progression", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Geometric Series". MathWorld.
- Geometric Series at PlanetMath.
- Peppard, Kim. "College Algebra Tutorial on Geometric Sequences and Series". West Texas A&M University.
- Casselman, Bill. "A Geometric Interpretation of the Geometric Series". Archived from the original (Applet) on 2007-09-29.
- "Geometric Series" by Michael Schreiber, Wolfram Demonstrations Project, 2007.

























