Inverse_function
Inverse function
Mathematical concept
In mathematics, the inverse function of a function f (also called the inverse of f) is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by
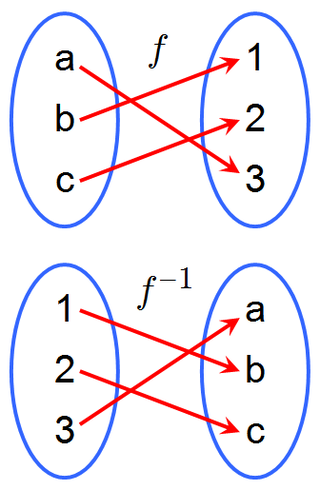
For a function 



As an example, consider the real-valued function of a real variable given by f(x) = 5x − 7. One can think of f as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of f is the function 
Let f be a function whose domain is the set X, and whose codomain is the set Y. Then f is invertible if there exists a function g from Y to X such that 



If f is invertible, then there is exactly one function g satisfying this property. The function g is called the inverse of f, and is usually denoted as f −1, a notation introduced by John Frederick William Herschel in 1813.[2][3][4][5][6][nb 1]
The function f is invertible if and only if it is bijective. This is because the condition 



The inverse function f −1 to f can be explicitly described as the function
.
Inverses and composition
Recall that if f is an invertible function with domain X and codomain Y, then
, for every
and
for every
.
Using the composition of functions, this statement can be rewritten to the following equations between functions:
and
where idX is the identity function on the set X; that is, the function that leaves its argument unchanged. In category theory, this statement is used as the definition of an inverse morphism.
Considering function composition helps to understand the notation f −1. Repeatedly composing a function f: X→X with itself is called iteration. If f is applied n times, starting with the value x, then this is written as f n(x); so f 2(x) = f (f (x)), etc. Since f −1(f (x)) = x, composing f −1 and f n yields f n−1, "undoing" the effect of one application of f.
Notation
While the notation f −1(x) might be misunderstood,[1] (f(x))−1 certainly denotes the multiplicative inverse of f(x) and has nothing to do with the inverse function of f.[6] The notation 
In keeping with the general notation, some English authors use expressions like sin−1(x) to denote the inverse of the sine function applied to x (actually a partial inverse; see below).[8][6] Other authors feel that this may be confused with the notation for the multiplicative inverse of sin (x), which can be denoted as (sin (x))−1.[6] To avoid any confusion, an inverse trigonometric function is often indicated by the prefix "arc" (for Latin arcus).[9][10] For instance, the inverse of the sine function is typically called the arcsine function, written as arcsin(x).[9][10] Similarly, the inverse of a hyperbolic function is indicated by the prefix "ar" (for Latin ārea).[10] For instance, the inverse of the hyperbolic sine function is typically written as arsinh(x).[10] The expressions like sin−1(x) can still be useful to distinguish the multivalued inverse from the partial inverse: 
Squaring and square root functions
The function f: R → [0,∞) given by f(x) = x2 is not injective because 

If the domain of the function is restricted to the nonnegative reals, that is, we take the function 

Standard inverse functions
The following table shows several standard functions and their inverses:
 ...
...| Function f(x) | Inverse f −1(y) | Notes |
|---|---|---|
| x + a | y − a | |
| a − x | a − y | |
| mx | y/m | m ≠ 0 |
| 1/x (i.e. x−1) | 1/y (i.e. y−1) | x, y ≠ 0 |
| xp | ![{\displaystyle {\sqrt[{p}]{y}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cb87b7b6c3375274b556888ab6f0c90f95fd91b9) (i.e. y1/p) (i.e. y1/p) |
x, y ≥ 0 if p is even; integer p > 0 |
| ax | loga y | y > 0 and a > 0 |
| xex | W (y) | x ≥ −1 and y ≥ −1/e |
| trigonometric functions | inverse trigonometric functions | various restrictions (see table below) |
| hyperbolic functions | inverse hyperbolic functions | various restrictions |
Formula for the inverse
Many functions given by algebraic formulas possess a formula for their inverse. This is because the inverse 

.
This allows one to easily determine inverses of many functions that are given by algebraic formulas. For example, if f is the function
then to determine 
Thus the inverse function f −1 is given by the formula
Sometimes, the inverse of a function cannot be expressed by a closed-form formula. For example, if f is the function
then f is a bijection, and therefore possesses an inverse function f −1. The formula for this inverse has an expression as an infinite sum:
Since a function is a special type of binary relation, many of the properties of an inverse function correspond to properties of converse relations.
Uniqueness
If an inverse function exists for a given function f, then it is unique.[13] This follows since the inverse function must be the converse relation, which is completely determined by f.
Symmetry
There is a symmetry between a function and its inverse. Specifically, if f is an invertible function with domain X and codomain Y, then its inverse f −1 has domain Y and image X, and the inverse of f −1 is the original function f. In symbols, for functions f:X → Y and f−1:Y → X,[13]
and
This statement is a consequence of the implication that for f to be invertible it must be bijective. The involutory nature of the inverse can be concisely expressed by[14]
The inverse of a composition of functions is given by[15]
Notice that the order of g and f have been reversed; to undo f followed by g, we must first undo g, and then undo f.
For example, let f(x) = 3x and let g(x) = x + 5. Then the composition g ∘ f is the function that first multiplies by three and then adds five,
To reverse this process, we must first subtract five, and then divide by three,
This is the composition (f −1 ∘ g −1)(x).
Self-inverses
If X is a set, then the identity function on X is its own inverse:
More generally, a function f : X → X is equal to its own inverse, if and only if the composition f ∘ f is equal to idX. Such a function is called an involution.
Graph of the inverse
If f is invertible, then the graph of the function
is the same as the graph of the equation
This is identical to the equation y = f(x) that defines the graph of f, except that the roles of x and y have been reversed. Thus the graph of f −1 can be obtained from the graph of f by switching the positions of the x and y axes. This is equivalent to reflecting the graph across the line y = x.[16][1]
Inverses and derivatives
The inverse function theorem states that a continuous function f is invertible on its range (image) if and only if it is either strictly increasing or decreasing (with no local maxima or minima). For example, the function
is invertible, since the derivative f′(x) = 3x2 + 1 is always positive.
If the function f is differentiable on an interval I and f′(x) ≠ 0 for each x ∈ I, then the inverse f −1 is differentiable on f(I).[17] If y = f(x), the derivative of the inverse is given by the inverse function theorem,
Using Leibniz's notation the formula above can be written as
This result follows from the chain rule (see the article on inverse functions and differentiation).
The inverse function theorem can be generalized to functions of several variables. Specifically, a differentiable multivariable function f : Rn → Rn is invertible in a neighborhood of a point p as long as the Jacobian matrix of f at p is invertible. In this case, the Jacobian of f −1 at f(p) is the matrix inverse of the Jacobian of f at p.
- Let f be the function that converts a temperature in degrees Celsius to a temperature in degrees Fahrenheit, then its inverse function converts degrees Fahrenheit to degrees Celsius,[18] since
- Suppose f assigns each child in a family its birth year. An inverse function would output which child was born in a given year. However, if the family has children born in the same year (for instance, twins or triplets, etc.) then the output cannot be known when the input is the common birth year. As well, if a year is given in which no child was born then a child cannot be named. But if each child was born in a separate year, and if we restrict attention to the three years in which a child was born, then we do have an inverse function. For example,
- Let R be the function that leads to an x percentage rise of some quantity, and F be the function producing an x percentage fall. Applied to $100 with x = 10%, we find that applying the first function followed by the second does not restore the original value of $100, demonstrating the fact that, despite appearances, these two functions are not inverses of each other.
- The formula to calculate the pH of a solution is pH = −log10[H+]. In many cases we need to find the concentration of acid from a pH measurement. The inverse function [H+] = 10−pH is used.
Partial inverses
Even if a function f is not one-to-one, it may be possible to define a partial inverse of f by restricting the domain. For example, the function
is not one-to-one, since x2 = (−x)2. However, the function becomes one-to-one if we restrict to the domain x ≥ 0, in which case
(If we instead restrict to the domain x ≤ 0, then the inverse is the negative of the square root of y.) Alternatively, there is no need to restrict the domain if we are content with the inverse being a multivalued function:
Sometimes, this multivalued inverse is called the full inverse of f, and the portions (such as √x and −√x) are called branches. The most important branch of a multivalued function (e.g. the positive square root) is called the principal branch, and its value at y is called the principal value of f −1(y).
For a continuous function on the real line, one branch is required between each pair of local extrema. For example, the inverse of a cubic function with a local maximum and a local minimum has three branches (see the adjacent picture).
These considerations are particularly important for defining the inverses of trigonometric functions. For example, the sine function is not one-to-one, since
for every real x (and more generally sin(x + 2πn) = sin(x) for every integer n). However, the sine is one-to-one on the interval [−π/2, π/2], and the corresponding partial inverse is called the arcsine. This is considered the principal branch of the inverse sine, so the principal value of the inverse sine is always between −π/2 and π/2. The following table describes the principal branch of each inverse trigonometric function:[19]
| function | Range of usual principal value |
|---|---|
| arcsin | −π/2 ≤ sin−1(x) ≤ π/2 |
| arccos | 0 ≤ cos−1(x) ≤ π |
| arctan | −π/2 < tan−1(x) < π/2 |
| arccot | 0 < cot−1(x) < π |
| arcsec | 0 ≤ sec−1(x) ≤ π |
| arccsc | −π/2 ≤ csc−1(x) ≤ π/2 |
Left and right inverses
Function composition on the left and on the right need not coincide. In general, the conditions
- "There exists g such that g(f(x))=x" and
- "There exists g such that f(g(x))=x"
imply different properties of f. For example, let f: R → [0, ∞) denote the squaring map, such that f(x) = x2 for all x in R, and let g: [0, ∞) → R denote the square root map, such that g(x) = √x for all x ≥ 0. Then f(g(x)) = x for all x in [0, ∞); that is, g is a right inverse to f. However, g is not a left inverse to f, since, e.g., g(f(−1)) = 1 ≠ −1.
Left inverses
If f: X → Y, a left inverse for f (or retraction of f ) is a function g: Y → X such that composing f with g from the left gives the identity function[20]

That is, the function g satisfies the rule
- If f(x)=y, then g(y)=x.
The function g must equal the inverse of f on the image of f, but may take any values for elements of Y not in the image.
A function f with nonempty domain is injective if and only if it has a left inverse.[21] An elementary proof runs as follows:
- If g is the left inverse of f, and f(x) = f(y), then g(f(x)) = g(f(y)) = x = y.
If nonempty f: X → Y is injective, construct a left inverse g: Y → X as follows: for all y ∈ Y, if y is in the image of f, then there exists x ∈ X such that f(x) = y. Let g(y) = x; this definition is unique because f is injective. Otherwise, let g(y) be an arbitrary element of X.
For all x ∈ X, f(x) is in the image of f. By construction, g(f(x)) = x, the condition for a left inverse.
In classical mathematics, every injective function f with a nonempty domain necessarily has a left inverse; however, this may fail in constructive mathematics. For instance, a left inverse of the inclusion {0,1} → R of the two-element set in the reals violates indecomposability by giving a retraction of the real line to the set {0,1}.[22]
Right inverses
A right inverse for f (or section of f ) is a function h: Y → X such that
That is, the function h satisfies the rule
- If
, then
Thus, h(y) may be any of the elements of X that map to y under f.
A function f has a right inverse if and only if it is surjective (though constructing such an inverse in general requires the axiom of choice).
- If h is the right inverse of f, then f is surjective. For all
, there is
such that
.
- If f is surjective, f has a right inverse h, which can be constructed as follows: for all
, there is at least one
such that
(because f is surjective), so we choose one to be the value of h(y).[citation needed]
Two-sided inverses
An inverse that is both a left and right inverse (a two-sided inverse), if it exists, must be unique. In fact, if a function has a left inverse and a right inverse, they are both the same two-sided inverse, so it can be called the inverse.
- If
is a left inverse and
a right inverse of
, for all
,
.
A function has a two-sided inverse if and only if it is bijective.
- A bijective function f is injective, so it has a left inverse (if f is the empty function,
is its own left inverse). f is surjective, so it has a right inverse. By the above, the left and right inverse are the same.
- If f has a two-sided inverse g, then g is a left inverse and right inverse of f, so f is injective and surjective.
Preimages
If f: X → Y is any function (not necessarily invertible), the preimage (or inverse image) of an element y ∈ Y is defined to be the set of all elements of X that map to y:
The preimage of y can be thought of as the image of y under the (multivalued) full inverse of the function f.
Similarly, if S is any subset of Y, the preimage of S, denoted 
For example, take the function f: R → R; x ↦ x2. This function is not invertible as it is not bijective, but preimages may be defined for subsets of the codomain, e.g.
.
The preimage of a single element y ∈ Y – a singleton set {y} – is sometimes called the fiber of y. When Y is the set of real numbers, it is common to refer to f −1({y}) as a level set.
- Lagrange inversion theorem, gives the Taylor series expansion of the inverse function of an analytic function
- Integral of inverse functions
- Inverse Fourier transform
- Reversible computing
- Not to be confused with numerical exponentiation such as taking the multiplicative inverse of a nonzero real number.
- Weisstein, Eric W. "Inverse Function". mathworld.wolfram.com. Retrieved 2020-09-08.
- Herschel, John Frederick William (1813) [1812-11-12]. "On a Remarkable Application of Cotes's Theorem". Philosophical Transactions of the Royal Society of London. 103 (Part 1). London: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall: 8–26 [10]. doi:10.1098/rstl.1813.0005. JSTOR 107384. S2CID 118124706.
- Herschel, John Frederick William (1820). "Part III. Section I. Examples of the Direct Method of Differences". A Collection of Examples of the Applications of the Calculus of Finite Differences. Cambridge, UK: Printed by J. Smith, sold by J. Deighton & sons. pp. 1–13 [5–6]. Archived from the original on 2020-08-04. Retrieved 2020-08-04. (NB. Inhere, Herschel refers to his 1813 work and mentions Hans Heinrich Bürmann's older work.)
- Peirce, Benjamin (1852). Curves, Functions and Forces. Vol. I (new ed.). Boston, USA. p. 203.
{{cite book}}: CS1 maint: location missing publisher (link) - Peano, Giuseppe (1903). Formulaire mathématique (in French). Vol. IV. p. 229.
- Cajori, Florian (1952) [March 1929]. "§472. The power of a logarithm / §473. Iterated logarithms / §533. John Herschel's notation for inverse functions / §535. Persistence of rival notations for inverse functions / §537. Powers of trigonometric functions". A History of Mathematical Notations. Vol. 2 (3rd corrected printing of 1929 issue, 2nd ed.). Chicago, USA: Open court publishing company. pp. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. Retrieved 2016-01-18.
[...] §473. Iterated logarithms [...] We note here the symbolism used by Pringsheim and Molk in their joint Encyclopédie article: "2logb a = logb (logb a), ..., k+1logb a = logb (klogb a)." [...] §533. John Herschel's notation for inverse functions, sin−1 x, tan−1 x, etc., was published by him in the Philosophical Transactions of London, for the year 1813. He says (p. 10): "This notation cos.−1 e must not be understood to signify 1/cos. e, but what is usually written thus, arc (cos.=e)." He admits that some authors use cos.m A for (cos. A)m, but he justifies his own notation by pointing out that since d2 x, Δ3 x, Σ2 x mean dd x, ΔΔΔ x, ΣΣ x, we ought to write sin.2 x for sin. sin. x, log.3 x for log. log. log. x. Just as we write d−n V=∫n V, we may write similarly sin.−1 x=arc (sin.=x), log.−1 x.=cx. Some years later Herschel explained that in 1813 he used fn(x), f−n(x), sin.−1 x, etc., "as he then supposed for the first time. The work of a German Analyst, Burmann, has, however, within these few months come to his knowledge, in which the same is explained at a considerably earlier date. He[Burmann], however, does not seem to have noticed the convenience of applying this idea to the inverse functions tan−1, etc., nor does he appear at all aware of the inverse calculus of functions to which it gives rise." Herschel adds, "The symmetry of this notation and above all the new and most extensive views it opens of the nature of analytical operations seem to authorize its universal adoption."[a] [...] §535. Persistence of rival notations for inverse function.— [...] The use of Herschel's notation underwent a slight change in Benjamin Peirce's books, to remove the chief objection to them; Peirce wrote: "cos[−1] x," "log[−1] x."[b] [...] §537. Powers of trigonometric functions.—Three principal notations have been used to denote, say, the square of sin x, namely, (sin x)2, sin x2, sin2 x. The prevailing notation at present is sin2 x, though the first is least likely to be misinterpreted. In the case of sin2 x two interpretations suggest themselves; first, sin x · sin x; second,[c] sin (sin x). As functions of the last type do not ordinarily present themselves, the danger of misinterpretation is very much less than in case of log2 x, where log x · log x and log (log x) are of frequent occurrence in analysis. [...] The notation sinn x for (sin x)n has been widely used and is now the prevailing one. [...]
(xviii+367+1 pages including 1 addenda page) (NB. ISBN and link for reprint of 2nd edition by Cosimo, Inc., New York, USA, 2013.) - Helmut Sieber und Leopold Huber: Mathematische Begriffe und Formeln für Sekundarstufe I und II der Gymnasien. Ernst Klett Verlag.
- Thomas 1972, pp. 304–309
- Korn, Grandino Arthur; Korn, Theresa M. (2000) [1961]. "21.2.-4. Inverse Trigonometric Functions". Mathematical handbook for scientists and engineers: Definitions, theorems, and formulars for reference and review (3 ed.). Mineola, New York, USA: Dover Publications, Inc. p. 811. ISBN 978-0-486-41147-7.
- Oldham, Keith B.; Myland, Jan C.; Spanier, Jerome (2009) [1987]. An Atlas of Functions: with Equator, the Atlas Function Calculator (2 ed.). Springer Science+Business Media, LLC. doi:10.1007/978-0-387-48807-3. ISBN 978-0-387-48806-6. LCCN 2008937525.
- Hall, Arthur Graham; Frink, Fred Goodrich (1909). "Article 14: Inverse trigonometric functions". Written at Ann Arbor, Michigan, USA. Plane Trigonometry. New York: Henry Holt & Company. pp. 15–16. Retrieved 2017-08-12.
α = arcsin m This notation is universally used in Europe and is fast gaining ground in this country. A less desirable symbol, α = sin-1 m, is still found in English and American texts. The notation α = inv sin m is perhaps better still on account of its general applicability. [...] A similar symbolic relation holds for the other trigonometric functions. It is frequently read 'arc-sine m' or 'anti-sine m', since two mutually inverse functions are said each to be the anti-function of the other.
- Smith, Eggen & St. Andre 2006, pg. 141 Theorem 3.3(a)
- Briggs & Cochran 2011, pp. 28–29
- "Inverse Functions". www.mathsisfun.com. Retrieved 2020-09-08.
- Briggs & Cochran 2011, pp. 39–42
- Dummit; Foote. Abstract Algebra.
- Mac Lane, Saunders. Categories for the Working Mathematician.
- Fraenkel (1954). "Abstract Set Theory". Nature. 173 (4412): 967. Bibcode:1954Natur.173..967C. doi:10.1038/173967a0. S2CID 7735523.
- Briggs, William; Cochran, Lyle (2011). Calculus / Early Transcendentals Single Variable. Addison-Wesley. ISBN 978-0-321-66414-3.
- Devlin, Keith J. (2004). Sets, Functions, and Logic / An Introduction to Abstract Mathematics (3 ed.). Chapman & Hall / CRC Mathematics. ISBN 978-1-58488-449-1.
- Fletcher, Peter; Patty, C. Wayne (1988). Foundations of Higher Mathematics. PWS-Kent. ISBN 0-87150-164-3.
- Lay, Steven R. (2006). Analysis / With an Introduction to Proof (4 ed.). Pearson / Prentice Hall. ISBN 978-0-13-148101-5.
- Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2006). A Transition to Advanced Mathematics (6 ed.). Thompson Brooks/Cole. ISBN 978-0-534-39900-9.
- Thomas Jr., George Brinton (1972). Calculus and Analytic Geometry Part 1: Functions of One Variable and Analytic Geometry (Alternate ed.). Addison-Wesley.
- Wolf, Robert S. (1998). Proof, Logic, and Conjecture / The Mathematician's Toolbox. W. H. Freeman and Co. ISBN 978-0-7167-3050-7.
- Amazigo, John C.; Rubenfeld, Lester A. (1980). "Implicit Functions; Jacobians; Inverse Functions". Advanced Calculus and its Applications to the Engineering and Physical Sciences. New York: Wiley. pp. 103–120. ISBN 0-471-04934-4.
- Binmore, Ken G. (1983). "Inverse Functions". Calculus. New York: Cambridge University Press. pp. 161–197. ISBN 0-521-28952-1.
- Spivak, Michael (1994). Calculus (3 ed.). Publish or Perish. ISBN 0-914098-89-6.
- Stewart, James (2002). Calculus (5 ed.). Brooks Cole. ISBN 978-0-534-39339-7.
 Definitions from Wiktionary
Definitions from Wiktionary Media from Commons
Media from Commons Textbooks from Wikibooks
Textbooks from Wikibooks Data from Wikidata
Data from Wikidata
- "Inverse function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]









![{\displaystyle {\begin{aligned}y&=(2x+8)^{3}\\{\sqrt[{3}]{y}}&=2x+8\\{\sqrt[{3}]{y}}-8&=2x\\{\dfrac {{\sqrt[{3}]{y}}-8}{2}}&=x.\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3107b63d271dd3e5b2f928a036c04525c896fbda)
![{\displaystyle f^{-1}(y)={\frac {{\sqrt[{3}]{y}}-8}{2}}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/82ff457f789a7a6b985416c9d82f04d89a8cf686)

![{\displaystyle f^{-1}(y)=\sum _{n=1}^{\infty }{\frac {y^{n/3}}{n!}}\lim _{\theta \to 0}\left({\frac {\mathrm {d} ^{\,n-1}}{\mathrm {d} \theta ^{\,n-1}}}\left({\frac {\theta }{\sqrt[{3}]{\theta -\sin(\theta )}}}\right)^{n}\right).}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1a3c7e1ed9b1858e0cfa36100898930fdc62c2dd)













![{\displaystyle {\begin{aligned}f^{-1}(f(C))={}&f^{-1}\left({\tfrac {9}{5}}C+32\right)={\tfrac {5}{9}}\left(({\tfrac {9}{5}}C+32)-32\right)=C,\\&{\text{for every value of }}C,{\text{ and }}\\[6pt]f\left(f^{-1}(F)\right)={}&f\left({\tfrac {5}{9}}(F-32)\right)={\tfrac {9}{5}}\left({\tfrac {5}{9}}(F-32)\right)+32=F,\\&{\text{for every value of }}F.\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f3f6b472e394206a93023c6ab3e619ef3d139280)


















