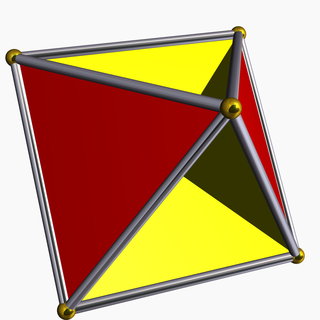
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U₄. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices.^[1] Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron).

Tetrahemihexahedron
Type	Uniform star polyhedron
Elements	F = 7, E = 12 V = 6 (χ = 1)
Faces by sides	4{3}+3{4}
Coxeter diagram	(double-covering)
Wythoff symbol	3/2 3 | 2 (double-covering)
Symmetry group	Td, [3,3], *332
Index references	U04, C36, W67
Dual polyhedron	Tetrahemihexacron
Vertex figure	3.4.3/2.4
Bowers acronym	Thah

The tetrahemihexahedron is the only non-prismatic uniform polyhedron with an odd number of faces. Its Wythoff symbol is 3/2 3 | 2, but that represents a double covering of the tetrahemihexahedron with eight triangles and six squares, paired and coinciding in space. (It can more intuitively be seen as two coinciding tetrahemihexahedra.)

The tetrahemihexahedron is a hemipolyhedron. The "hemi" part of the name means some of the faces form a group with half as many members as some regular polyhedron—here, three square faces form a group with half as many faces as the regular hexahedron, better known as the cube—hence hemihexahedron. Hemi faces are also oriented in the same direction as the regular polyhedron's faces. The three square faces of the tetrahemihexahedron are, like the three facial orientations of the cube, mutually perpendicular.

The "half-as-many" characteristic also means that hemi faces must pass through the center of the polyhedron, where they all intersect each other. Visually, each square is divided into four right triangles, with two visible from each side.

The tetrahemihexahedron is a non-orientable surface. It is unique as the only uniform polyhedron with an Euler characteristic of 1 and is hence a projective polyhedron, yielding a representation of the real projective plane^[2] very similar to the Roman surface.

Roman surface

The tetrahemihexahedron has the same vertices and edges as the regular octahedron. It also shares 4 of the 8 triangular faces of the octahedron, but has three additional square faces passing through the centre of the polyhedron.

The dual figure of the tetrahemihexahedron is the tetrahemihexacron.

The tetrahemihexahedron is 2-covered by the cuboctahedron,^[2] which accordingly has the same abstract vertex figure (2 triangles and two squares: 3.4.3.4) and twice the vertices, edges, and faces. It has the same topology as the abstract polyhedron hemi-cuboctahedron.

The tetrahemihexahedron may also be constructed as a crossed triangular cuploid. All cuploids and their duals are topologically projective planes.^[3]