Unit_vector
Unit vector
Vector of length one
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in 
The term direction vector, commonly denoted as d, is used to describe a unit vector being used to represent spatial direction and relative direction. 2D spatial directions are numerically equivalent to points on the unit circle and spatial directions in 3D are equivalent to a point on the unit sphere.
The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e.,
where ‖u‖ is the norm (or length) of u.[1][2] The term normalized vector is sometimes used as a synonym for unit vector.
Unit vectors are often chosen to form the basis of a vector space, and every vector in the space may be written as a linear combination of unit vectors.
Cartesian coordinates
Unit vectors may be used to represent the axes of a Cartesian coordinate system. For instance, the standard unit vectors in the direction of the x, y, and z axes of a three dimensional Cartesian coordinate system are
They form a set of mutually orthogonal unit vectors, typically referred to as a standard basis in linear algebra.
They are often denoted using common vector notation (e.g., x or 



When a unit vector in space is expressed in Cartesian notation as a linear combination of x, y, z, its three scalar components can be referred to as direction cosines. The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector. This is one of the methods used to describe the orientation (angular position) of a straight line, segment of straight line, oriented axis, or segment of oriented axis (vector).
Cylindrical coordinates
The three orthogonal unit vectors appropriate to cylindrical symmetry are:
(also designated
or
), representing the direction along which the distance of the point from the axis of symmetry is measured;
, representing the direction of the motion that would be observed if the point were rotating counterclockwise about the symmetry axis;
, representing the direction of the symmetry axis;
They are related to the Cartesian basis 


The vectors 



Spherical coordinates
The unit vectors appropriate to spherical symmetry are: 






The spherical unit vectors depend on both 

General unit vectors
Common themes of unit vectors occur throughout physics and geometry:[4]
 , A normal vector ...
, A normal vector ...| Unit vector | Nomenclature | Diagram |
|---|---|---|
| Tangent vector to a curve/flux line |  |  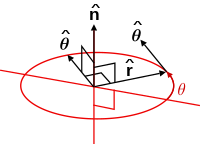
A normal vector |
| Normal to a surface tangent plane/plane containing radial position component and angular tangential component | 
In terms of polar coordinates;
| |
| Binormal vector to tangent and normal |  [5] [5] | |
| Parallel to some axis/line |  | 
One unit vector |
| Perpendicular to some axis/line in some radial direction |  | |
| Possible angular deviation relative to some axis/line |  |

Unit vector at acute deviation angle φ (including 0 or π/2 rad) relative to a principal direction. |
In general, a coordinate system may be uniquely specified using a number of linearly independent unit vectors 

where 

A unit vector in 





Thus the right versors extend the notion of imaginary units found in the complex plane, where the right versors now range over the 2-sphere 
By extension, a right quaternion is a real multiple of a right versor.
- Weisstein, Eric W. "Unit Vector". mathworld.wolfram.com. Retrieved 2020-08-19.
- "Unit Vectors | Brilliant Math & Science Wiki". brilliant.org. Retrieved 2020-08-19.
- Tevian Dray and Corinne A. Manogue, Spherical Coordinates, College Math Journal 34, 168-169 (2003).
- F. Ayres; E. Mendelson (2009). Calculus (Schaum's Outlines Series) (5th ed.). Mc Graw Hill. ISBN 978-0-07-150861-2.
- M. R. Spiegel; S. Lipschutz; D. Spellman (2009). Vector Analysis (Schaum's Outlines Series) (2nd ed.). Mc Graw Hill. ISBN 978-0-07-161545-7.
- G. B. Arfken & H. J. Weber (2000). Mathematical Methods for Physicists (5th ed.). Academic Press. ISBN 0-12-059825-6.
- Spiegel, Murray R. (1998). Schaum's Outlines: Mathematical Handbook of Formulas and Tables (2nd ed.). McGraw-Hill. ISBN 0-07-038203-4.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.























