In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U₃₆.^[1] It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).

Dodecadodecahedron
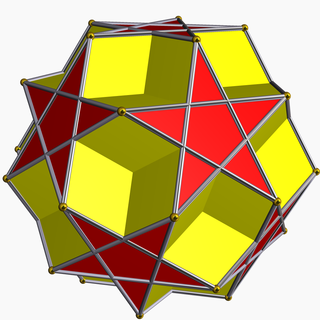Type	Uniform star polyhedron
Elements	F = 24, E = 60 V = 30 (χ = −6)
Faces by sides	12{5}+12{5/2}
Coxeter diagram
Wythoff symbol	2 | 5 5/2 2 | 5 5/3 2 | 5/2 5/4 2 | 5/3 5/4
Symmetry group	Ih, [5,3], *532
Index references	U36, C45, W73
Dual polyhedron	Medial rhombic triacontahedron
Vertex figure	5.5/2.5.5/2
Bowers acronym	Did

The edges of this model form 10 central hexagons, and these, projected onto a sphere, become 10 great circles. These 10, along with the great circles from projections of two other polyhedra, form the 31 great circles of the spherical icosahedron used in construction of geodesic domes.

It has four Wythoff constructions between four Schwarz triangle families: 2 | 5 5/2, 2 | 5 5/3, 2 | 5/2 5/4, 2 | 5/3 5/4, but represent identical results. Similarly it can be given four extended Schläfli symbols: r{5/2,5}, r{5/3,5}, r{5/2,5/4}, and r{5/3,5/4} or as Coxeter-Dynkin diagrams: , , , and .

A shape with the same exterior appearance as the dodecadodecahedron can be constructed by folding up these nets:

12 pentagrams and 20 rhombic clusters are necessary. However, this construction replaces the crossing pentagonal faces of the dodecadodecahedron with non-crossing sets of rhombi, so it does not produce the same internal structure.

Its convex hull is the icosidodecahedron. It also shares its edge arrangement with the small dodecahemicosahedron (having the pentagrammic faces in common), and with the great dodecahemicosahedron (having the pentagonal faces in common).

This polyhedron can be considered a rectified great dodecahedron. It is center of a truncation sequence between a small stellated dodecahedron and great dodecahedron:

The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces: 12 pentagons from the truncated vertices and 12 overlapping as (truncated pentagrams). The truncation of the dodecadodecahedron itself is not uniform and attempting to make it uniform results in a degenerate polyhedron (that looks like a small rhombidodecahedron with {10/2} polygons filling up the dodecahedral set of holes), but it has a uniform quasitruncation, the truncated dodecadodecahedron.

More information Name, Small stellated dodecahedron ...

Name	Small stellated dodecahedron	Truncated small stellated dodecahedron	Dodecadodecahedron	Truncated great dodecahedron	Great dodecahedron
Coxeter-Dynkin diagram
Picture

Close

It is topologically equivalent to a quotient space of the hyperbolic order-4 pentagonal tiling, by distorting the pentagrams back into regular pentagons. As such, it is topologically a regular polyhedron of index two:^[2][3]

• List of uniform polyhedra