Coronavirus is growing exponentially – here’s what that really means
The awesome power of exponential growth explained.
April 3, 2020 • 7 min • Source
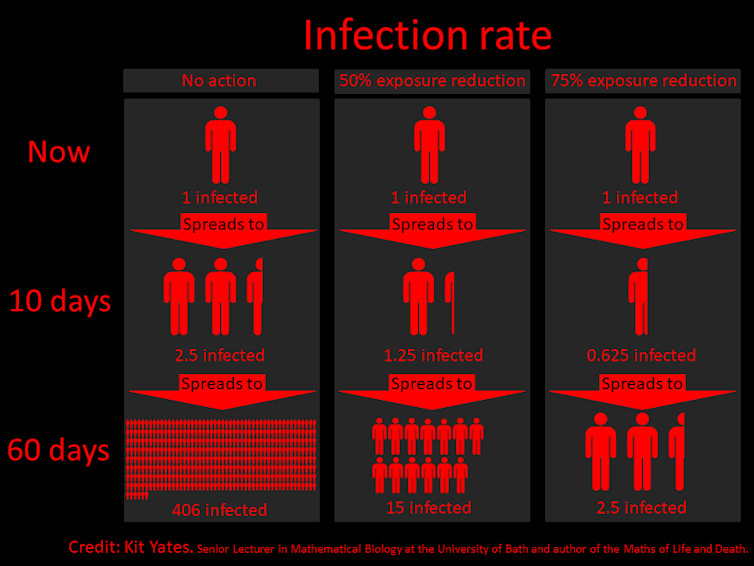
You may have seen a version of the infographic (below) that explains the potential impact of social distancing. It nicely illustrates that reducing the total number of disease-spreading contacts each infected person has can have a dramatic effect on the total number of infections a short time later. The numbers rely on the mathematical concept of “exponential growth”.
Recently, Boris Johnson, THE British prime minister, told the press that “it looks as though we’re now approaching the fast growth part of the upward curve. And without drastic action, cases could double every five or six days”. The consistent doubling of cases in a fixed period is the hallmark of exponential growth.
The number of new infections that a single infectious individual will cause during their infectious period is known as the basic reproduction number of a disease. This number is key to determining how widespread a disease will become.
For COVID-19, early estimates of the basic reproduction number have it somewhere between 1.5 and 4. The infographic assumes a figure somewhere in the middle, at 2.5 infectious contacts per infectious individual.
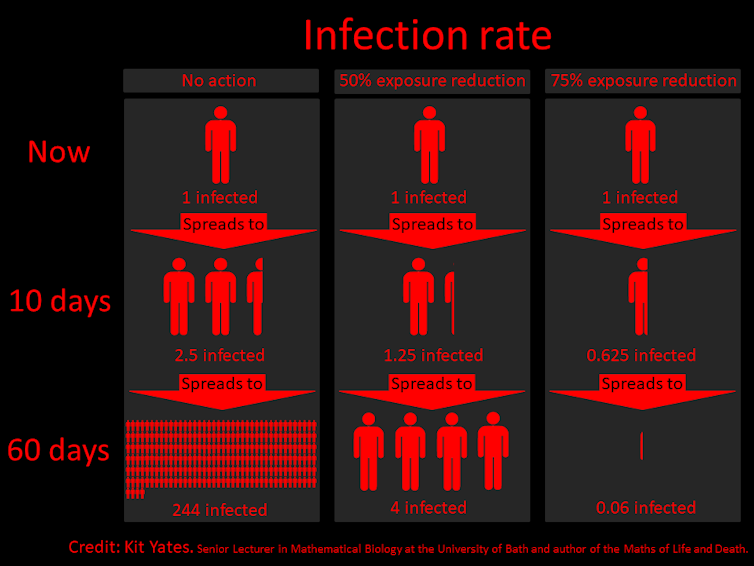
If the reproduction number of a disease can be brought below one, then the spread will slow until the disease dies out. The revised infographic below shows the number of currently infected people. Reducing contact with others by 75% will bring the reproduction number below the critical level, allowing the number of infected people to decrease almost to 0 in just two months.
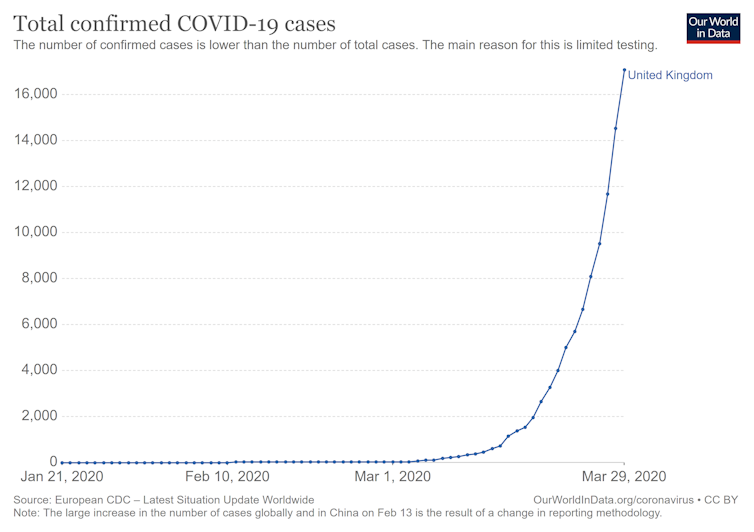
However, the basic reproduction number of the current stage of the outbreak is way above 1. This means that each newly infected person will pass on the disease to at least one more person, on average, and consequently the disease will take off exponentially.
What exponential growth is
But what, precisely, is exponential growth? The mathematical definition says that a quantity that increases with a rate proportional to its current size will grow exponentially. This means that as the quantity increases so does that rate at which it grows. The more infected people we have in the early stages of a disease outbreak, the more people they will infect and the more the cases will rise.
Other situations in which exponential growth plays a critical role range from pyramid schemes to nuclear weapons. In a pyramid scheme, each new investor invites two more recruits who in turn invite two more. This rapid growth, at a rate proportional to the current number of members, inevitably leads to a situation in which there aren’t enough new recruits to keep the scheme going and it eventually collapses. When the pyramid tumbles, most investors lose their money.
In a nuclear fission bomb, a single uranium atom splits in two, jettisoning fast-moving neutrons and large quantities of energy in the form of electromagnetic radiation. The neutrons then collide with more atomic nuclei, splitting more atoms and releasing yet more energy in a nuclear chain reaction that increases exponentially.
At about 8:15 in the morning of August 6 1945, the atomic bomb known as the Little Boy detonated releasing energy equivalent to 30 million sticks of dynamite in an instant, devastating the Japanese city of Hiroshima. The surrender of Imperial Japan was announced nine days later. This is the awesome power of exponential growth.
What exponential growth isn’t
Although the concept of exponential growth is not new in the public consciousness, a lot of misconceptions surround the idea. Exponential is often used as a byword for rapid or large. As a counterpoint, consider the money in your bank account. Provided the interest is compounded (that is, interest is added to your initial amount and earns interest itself) then the total amount of money in your account increases in proportion to its current size – the hallmark of exponential growth.
As Benjamin Franklin put it: “Money makes money, and the money that money makes, makes more money.” If you could wait long enough, even the smallest investment would become a fortune. But don’t lock up your rainy-day fund just yet. If you invested £100 at 1% per year it would take you over 900 years to become a millionaire. Very few people would accuse the exponential growth associated with their bank account of being large or rapid.
So exponential growth does not necessarily deal with big quantities, and it is not necessarily fast. Unfortunately, across a wide range of different countries, the term exponential is appropriate to describe the rapid spread of SARS-CoV-2, the virus that causes COVID-19. With cases doubling every three to four days in the UK and deaths doubling every two to three days, things could get ugly quickly.
Small comfort
One small crumb of comfort is that almost nothing can grow exponentially forever. The only exception, ironically, is the all-too-slow growth of money in your bank account, which, at least on paper, could grow indefinitely. Unfortunately, COVID-19 cases don’t have to grow exponentially forever, or even for much longer, before the disease becomes one of the most devastating pandemics the world has ever seen.
Because the exponential proliferation of the disease is so undeniably dramatic, any changes we can make at this relatively early stage can make a huge difference even a few days down the line. Now is the time to act, to “double down” on our containment efforts to bring the exponential spread under control.
Christian Yates does not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and has disclosed no relevant affiliations beyond their academic appointment.